Besaran Vektor dan Skalar

Besaran Vektor dan besaran Skalar Penulis : Yoskin Erlangga Anwarsyam

Dalam pembahasan sebelumnya, mengenai Besaran dan Satuan, anda sudah mempelajari besaran Fisika, seperti besaran pokok dan besaran turunan. Dalam bab (halaman blog) ini, anda saya ajak untuk memahami kelompok besaran Fisika lainnya, yaitu Besaran Vektor dan Besaran Skalar.

Besaran Skalar

Pada saat anda menghitung luas sebuah bidang bujur sangkar, maka anda hanya menyebut angka (nilai) nya saja, misalkan 25 cm² Demikian pula, saat anda membeli dan menimbang satu keranjang buah mangga, maka pada timbangan tertera angka yang menunjukkan massa mangga tersebut, misalkan 4 kg.

Pada contoh tersebut diatas, besaran Luas bujur sangkar dan Massa mangga merupakan besaran skalar, yaitu besaran yang hanya memilik besar (nilai) saja dan tidak memiliki arah.

Contoh besaran Skalar yaitu, panjang, massa, waktu, suhu, massa jenis, volume, enegi potensial, usaha, potensial listrik, energi listrik dan lainsebagainya.

Besaran Vektor

Jika sebuah mangga yang anda beli tadi, berada dalam genggaman tangan anda, yang semula diam, kemudian terjatuh. Apa yang anda amati? Buah mangga tersebut jatuh kearah lantai, yang disebabkan oleh Gravitasi Bumi (Gaya). Pada gerak mangga, dari keadaan diam bergerak dengan kecepatan yang terus bertambah dengan arah kebawah hingga menyentuh lantai. Dari kejadian tersebut, kita dapat menyebutkan bahwa, besaran Gaya dan besaran Kecepatan merupakan besaran Vektor, yaitu besaran yang memilik nilai dan arah.

Vektor dapat dituliskan dalam huruf kecil dan besar, atau dengan dua huruf seperti berikut :

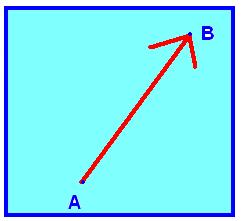
Sebuah vektor digambarkan dengan sebuah anak panah (lihat gambar), yaitu panjang panah menunjukkan nilai atau besarnya vektor dan arah anak panah menunjukkan arah vektor
Keterangan :
Titik A : adalah titik awal ( titik tangkap ) vektor
Titik B : adalah arah vektor
Panjang AB merupakan panjang atau besar vektor

Tabel Beberapa Contoh
Besaran Skalar dan Besaran Vektor :

NO	BESARAN SKALAR	BESARAN VEKTOR
1	JARAK	PERPINDAHAN
2	MASSA	BERAT
3	PANJANG	PERCEPATAN
4	KELAJUAN	KECEPATAN
5	VOLUME	PERCEPATAN GRAVITASI
6	WAKTU	MOMENTUM
7	ENERGI POTENSIAL	IMPULS
8	ENERGI KINETIK	GAYA
9	USAHA	MOMEN GAYA
10	DAYA	TEGANGAN PERMUKAAN
11	MASSA JENIS	GAYA GESEK
12	MUATAN LISTRIK	INDUKSI MAGNETIK
13	POTENSIAL LISTRIK	MEDAN GRAVITASI
14	JUMLAH ZAT	MEDAN LISTRIK
15	KERAPATAN ARUS	TEKANAN

Komponen Vektor :

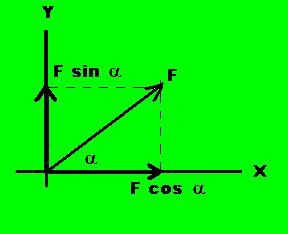
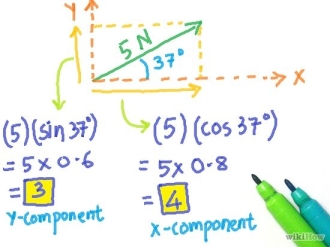
Sebuah vektor F berada dalam bidang datar yang membentuk sudut α terhadap sumbu X (lihat gambar). Vektor tersebut jika diproyeksikan terhadap sumbu X dan sumbu Y akan memiliki komponen-komponen vektor terhadap sumbu-sumbu tersebut, yaitu Fx dan Fy

Persamaan komponen vektor tersebut :

Fx = F cos α

Fy = F sin α

Contoh Soal :

Komponen-komponen vektor dari gambar vektor berikut adalah…

A. Ax = -4 N dan Ay = 3 N
B. Ax = -3 N dan Ay = 4 N
C. Ax = 3 N dan Ay = 4 N
D. Ax = 4 N dan Ay = 3 N
E. Ax = 5 N dan Ay = 5 N

Jawab : D

Sumber gambar : http://www.wikihow.com/Resolve-a-Vector-Into-Components

Aplikasi Vektor :

Dalam kehidupan sehari-hari banyak kita jumpai aplikasi vektor, contoh sederhana adalah sebuah benda yang jatuh dari tangan anda kebawah lantai. Dalam hal ini benda jatuh akibat Gravitasi bumi (gaya tarik bumi) yang arahnya menuju pusat bumi. Hal ini juga menunjukkan benda mmiliki berat yang arah dan besarnya sama dengan gaya tarik bumi terhadap benda tersebut.

Contoh lain dapat anda lihat dalam gambar berikut :

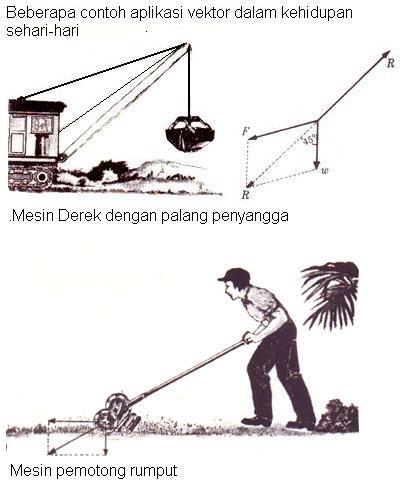
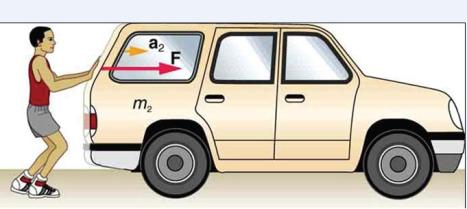                                        Mendorong Mobil.

Sumber gambar : http://cnx.org/content/m42073/latest/?collection=col11406/latest

Pada mesin derek palang penyangga menahan gaya berat beban (w ) dan gaya tarik tali (F)) . dengan gaya dorong palang penyangga R. Pada mesin pemotong rumput, seorang pekerja mendorong mesin dengan gaya F. Pada gambar selanjutnya, seseorang mendorong mobil dengan gaya F yang menimbulkan percepatan a

Operasi Vektor :

Dalam penggunaan Vektor, dua buah vektor atau lebih dapat dijumlah, dikurang, dikalikan atau dibagi. Kegiatan ini disebut Operasi vektor.

Penjumlahan dan pengurangan Vektor.

Menjumlahkan dan mengurangkan Vektor dapat ditempuh dengan 2 (dua) cara yaitu :
1. Metode grafis seperti metode Polygon, Jajaran Genjang dan Segitiga
2. Metode Analitis, yaitu menguraikan vektor2 yang ada terhadap sumbu X dan 
sumbu Y
Hasil dari penjumlahan vektor-vektor disebut Resultan Vektor (R)

Metode Grafis :

1. Cara Polygon.

Gambar (1) menunjukkan 3(tiga) buah vektor, yaitu vektor a, b dan vektor c.
Resultan Vektornya dapat anda lihat pada gambar (2)

Gambar (1) : vektor a, b dan c

dengan Resultan Vektor ( R) adalah R = a + b + c

Gbr(2). Resultan Vektor (R)

Jika R = a + b + c + d (gbr.3) maka besar R adalah = nol

Gbr (3). Resultan Vektor R = nol

2. Cara Jajaran Genjang

Penjumlahan dan pengurangan 2 buah vektor A dan B yang satu sama lain membentuk sudut α dapat dilihat pada gambar berikut ini.

Dari gbr (p) penjumlahan vektor A + B dan gbr (q) adalah pengurangan vektor A – B mempunyai persamaan :

Dari Gbr (p) : Penjumlahan vektor A + B menghasilkan resultan vektor R
Dari Gbr (q) : Pengurangan vektor A – B menghasilkan resultan vektor R dengan persamaan /
rumus tanda (+) dan (-) yang berbeda

 Metode Analitis :

Penjumlahan/pengurangan vektor dengan metode analitis adalah menjumlahkan beberapa vektor yang ada dengan menguraikan vektor-vektor tersebut terlebih dahulu terhadap sumbu X dan Y, kemudian nilainya dimasukkan ke dalam tabel X dan Y dan diselesaikan dengan persamaan :

Contoh :
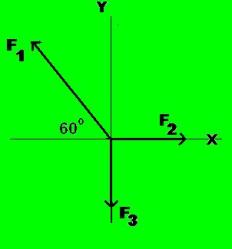
Tiga buah gaya bekerja pada sistem koordinat XY (lihat gambar).
Jika F1 = 8 N, F2 = 4 N dan F3 = 3√3 N ,  maka Resultan gaya yang bekerja pada sistem adalah …

A. 8 N
B. 5√3 N
C. 4√2 N
D. 2√2 N
E. √3 N
Jawab : E

Penyelesaiaan :

Uraikan dulu vektor F1 terhadap sumbu X dan sumbu Y (lihat gbr). Kemudian isikan kedalam tabel

Arah Resultan Vektor Ө dapat dicari dengan persamaan tg Ө = ∑Y/∑X.  Dari soal diatas diperoleh Ө = 60·

MACAM – MACAM ALAT UKUR

 

 

 

 

 

 

157 Votes

1.Mistar baja
mistar baja yaitu alat yang digunakan untuk mengukur dimensi panjang, lebar, dan tebal. Ketelitiannya adalah ± 0,5 mm.

Dalam membaca skala pada mistar, mata harus tegak lurus dengan skala yang akan dibaca.
Cara penggunaanya:
– Rapatkan benda ukur pada landasan tumpuan atau balok landas.
– Letakkan mistar baja diatas benda ukur, letakkan titik nol atau ujung mistar baja pada balok landas.
– Baca dimensi atau ukuran panjang benda ukur.

2.Micrometer sekrup
micrometer sekrup ini biasanya digunakan untuk mengukur ketebalan suatu benda, diameter, dll. Misalnya mengukur ketebalan kertas dan mengukur diameter kawat.

Cara Penggunaanya:
– Pastikan pengunci dalam keadaan terbuka
– Buka rahan dengan cara memutar kekiri pada skala putar hingga benda dapat masuk kerahang.
– Letakkan benda yang diukur pada rahang, dan putar kembali sampai tepat.

3.Ampere Meter
Amperemeter adalah suatu alat yang digunakan untuk mengukur kuat arus listrik. Pada umumnya alat ini dipakai oleh teknisi elektronik yang biasanya terletak pada alat multitester listrik yaitu gabungan amperemeter, voltmeter dan ohm meter.

4.Voltmeter
Voltmeter alat yang digunakan untuk mengukur tegangan listrik. Dengan ditambah alat multiplier akan dapat meningkatkan kemampuan pengukuran alat voltmeter berkali-kali lipat.

5.Ohmmeter
Ohmmeter ialah alat yag digunakan untuk mengukur hambata listrik yang merupakan suatu daya yang mampu menahan aliran listrik pada konduktor. Alat tersebut menggunakan galvanometer untuk melihat besarnya arus listrik yang kemudian dikalibrasi kesatuan ohm.

6.Thermometer
Thermometer adalah alat untuk mengukur suhu, baik suhu udara maupun suhu air. Satuan umum yang digunakan adalah celcius.

Cara penggunaanya:
thermometer bekerja berdasarkan perubahan kuantitas fisik, ketika temperaturnya berubah. Jadi bisa berdasarkan pemuaian (thermometer air raksa), perubahan resistivitas, perubahan kuantitas listrik(termokopel), radiasi bahan (thermometer temperature tinggi).

7.Jangka sorong

jangka sorong ialah suatu alat ukur yang digunakan untuk mengukur panjang suatu benda dengan ketelitian hingga 0,1mm.

kegunaan jangka sorong adalah:
– untuk mengukur suatu benda dari sisi luar dengan cara diapit,
– untuk mengukur sisi dalam suatu benda yang biasanya beruapa lubang( pada pipa, maupun yang lainnya) dengan cara di ulur,
– untuk mengukur kedalaman celah/lubang pada suatu benda dengan cara menancapkan atau menusukkan di bagian pengukur.

8.Barometer
barometer merupakan alat pengukur tekanan udara dalam satuan Mb. Barometer termasuk peralatan meteorology golongan non recording yang pada waktu tertentu harus dibaca agar mendapat data yang diinginkan.

9.Stopwatch
stopwatch adalah alat yang digunakan untuk mengukur lamanya waktu yang diperlukan dalam kegiatan, misalnya: berapa lama waktu yang ditemuh si pelari dalam jarak 100 M.

cara penggunaanya: tombol start, stop dan reset yang dipergunakan untuk memulai, menghentikan dan mengulang pengukuran waktu.
skala yang digunakan:
1. dalam detik, skala ini disusun melingkar di bagian pinggir dengan jarak antar skala 0,2 detik. Jarum panjang ialah yang berfungsi untuk pengukuran dalam detik.
2. Dalam menit, skala ini disusun melingkar dengan jarak antar skala 1 menit. Jarum pendek berfungsiuntuk penunjuk waktu dalam menit.

10.Speedometer
speedometer adalah alat pengukur kecepatan kendaraan darat, yang merupakan perlengkapan standar setiap kendaraan yang beroperasi dijalan.

cara kerjanya : perangkat pengukur kecepatan yang dihubungkan langsung dengan roda depan ataupun transmisi dengan menggunakan suatu kabelyang ikut berputar saat kendaraan bergerak, gerakan berputar ini kemudian di ubah untuk menggerakkanjarak kecepatan.

11.Hygrometer
hygrometer adalah alat untuk mengukur tingkat kelembapan pada suatu tempat.

Cara penggunaanya : alat ini ditempatkan didalam kotak penyimpanan barang yang memerlukan tahap kelembapan yang terjaga seperti dry box penyimpanan kamera. Kelembapan yang rendah akan mencegah bertumbuhnya jamur yang menjadi musuh pada peralatn tersebut.

12.Manometer
Manometer adalah alat pengukur tekanan udara di dalam ruang tertutup.

Penggunaannya:
Manometer digunakan untuk menentukan perbedaan tekanan diantara dua titik disaluran pembuangan gas atau udara. Perbedaan tekenan kemudian digunakan untuk menghitung kecepatan aliran disaluran dengan menggunakan persamaan Bernoulli (perbedaan tekanan = V2/2g).

13.Densimeter
Densimeter adala alat yang digunakan untuk mengukur kerapatan zat cair secara langsung.

Cara penggunaan:
Densimeter dimasukkan kedalam sampel. Pastikan densimeter tidak boleh menyentuh dasar dan dinding pada wadah sampel (misalnya gelas ukur). Jika densimeter masih menyentuh dinding maka densimeter harus diputar sehingga posisinya tepat ditengah.

14.Anonemeter meter
Anemometer adalah alat yang digunakan untuk mengukur kecepatan angin yang banyak dipakai dalam bidang meteorology dan geofisika atau stasiun perkiraan cuaca.

Cara penggunaan:
Anemometer harus ditempatkan di daerah terbuka. Pada saat tertiup angin baling-baling yang terdapat pada anemometer akan bergerak sesuai arah mata angin. Didalam anemometer terdapat alat pencatat kecepatan angin. Maka dengan itu kita dapat memperoleh kecepatannya berapa.

15.Altimeter
Altimeter adakah alat untuk mengukur ketinggian suatu titik dari permukaan laut. Biasanya alat ini digunakan untuk navigasi dalam penerbangan, pendakian, dan kegiatan yang berhubungan dengan ketinggian.

Altimeter bekerja dengan beberapa prinsip:
– Tekanan udara
– Magnet bumi
– Gelombang.
Penggunaan altimeter umumnya selalu diikuti dengan kompas.

16.Meteran pita
Meteran pita adalah alat yang digunakan untuk mengukur panjang benda atau sebagainya. Meteran pita ini untuk mengukur suatu obyek yang tidak bisa dilakukan dengan mistar.

17.Luxmeter
Luxmeter adalah alat yang digunakan untuk mengukur tingkat pencahayaan suatu ruangan.

Cara penggunaanya:
System kerja dari peralatan luxmeter menggunakan sensor cahaya. Alat tersebut cukup di letakkan diatas meja atau jug bisa dipegang setinggi 75cm dari atas permukaan lantai. Maka layar penunjuk dari luxmeter tersebut akan menunjukkan angka yang merupakan nilai dari intensitas pencahayaan ruangan yang bersangkutan.

18.Antique caliper ( alat ukur diameter tua )

Alat ukur ini diproduksi pada tahun 1930-an ini masih memakai teknologi sederhana , jauh sebelum vernier caliper ( baik yang manual maupun digital ) di temukan. Capit dari besi bisa direnggangkan dan terkunci rapat sesuai panjang barang yang akan di ukur. Sangat cocok untuk mengukur diameter benda – benda yang susah diukur langsung penggaris biasa , misalnya mengukur transisi leher botol.

19.Echosounder
Echosounder adalah alat untuk mengukur kedalaman air dengan mengirimkan tekanan gelombang dari permukaan ke dasar air dan di catat hasilnya sampai echo kembali kedasar air.

Prinsip kerjanya yaitu: pada transmitter terdapat tranduser yang berfungsi untuk merubah energy listrik menjadi energy suara. Kemudian suara yang di hasilkan dipancarkan dengan frequensi tertentu.

20.Ombrometer
Ombrometer adalah alat untuk mengukur curah hujan.

Cara penggunaan ombrometer yang manual adalah dengan menampung hujan yang terjadi pada setiap jam pengamatan alat akan di lepas dan air hujan ditakar dengan menggunakan gelas ukur. Prinsip kerja alat manual ini adalah menghitung besar air yang ditampung pada alat dan di ukur dengan gelas ukur.

Sumber : https://wandasaputra93.wordpress.com/2014/01/12/macam-macam-alat-ukur/